Container With Most Water
Problem
Given n non-negative integers a1, a2, …, an , where each represents a point at coordinate (i, ai). n vertical lines are drawn such that the two endpoints of line i is at (i, ai) and (i, 0). Find two lines, which together with x-axis forms a container, such that the container contains the most water.
Note
- You may not slant the container and n is at least 2.
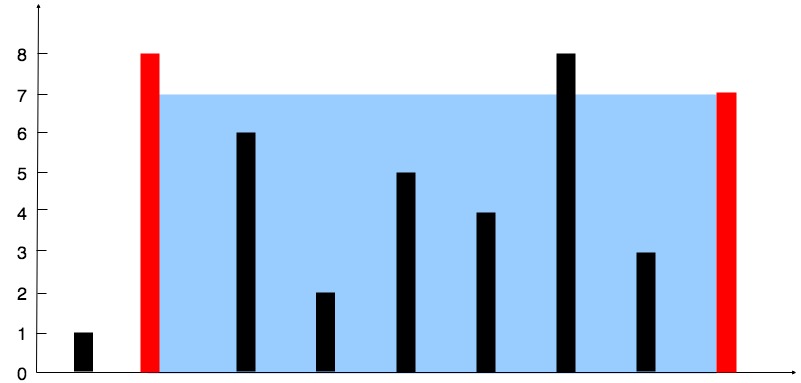
The above vertical lines are represented by array [1,8,6,2,5,4,8,3,7]. In this case, the max area of water (blue section) the container can contain is 49.
Example
1
2
Input: [1,8,6,2,5,4,8,3,7]
Output: 49
My Answer
- height 배열을 순회 하면서 각 영역 별 최대 값을 구하고, 비교한다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public int maxArea(int[] height) {
int max = 0;
for(int i=0;i < height.length - 1;i++) {
int L = height[i];
for(int j = i + 1; j < height.length; j++) {
int R = height[j];
int min = L > R ? R : L;
int n_total = (j - i) * min;
if ( n_total > max )
max = n_total;
}
}
return max;
}
}
Fastest Answer
- 좌, 우 끝단 부터 시작 해서 최대 값을 구한다.
- Explain
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public int maxArea(int[] height) {
int left=0;
int right=height.length-1;
int most=0;
while (left < right) {
int min = height[left] < height[right] ? height[left] : height[right];
most = Math.max(most, min * (right - left));
if (height[left] < height[right]) {
int oldLeft = height[left];
while (height[left] <= oldLeft && left < right) {
left++;
}
}else{
int oldRight = height[right];
while (height[right] <= oldRight && left < right) {
right--;
}
}
}
return most;
}
}