Lowest Common Ancestor of a Binary Search Tree
Problem
Given a binary search tree (BST), find the lowest common ancestor (LCA) of two given nodes in the BST.
According to the definition of LCA on Wikipedia: “The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).”
Given binary search tree: root = [6,2,8,0,4,7,9,null,null,3,5]
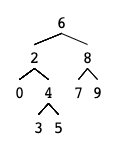
Example 1
1
2
3
Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
Output: 6
Explanation: The LCA of nodes 2 and 8 is 6.
Example 2
1
2
3
Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
Output: 2
Explanation: The LCA of nodes 2 and 4 is 2, since a node can be a descendant of itself according to the LCA definition.
Note
- All of the nodes’ values will be unique
- p and q are different and both values will exist in the BST.
My Answer
BST의 특징을 이용하자.p와q중에 큰 값(b)와 작은 값(s)가 무엇인지 다음의 조건을 이용해서 확인.- 만약 라면
root가LCA이다. - 만약 라면
root.left를 기준으로 다시1번 조건을 만족하는지 확인해야 한다. - 만약 라면
root.right를 기준으로 다시1번 조건을 만족하는지 확인해야 한다.
- 만약 라면
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
int min = 0;
int max = 0;
if ( p.val > q.val ) {
min = q.val;
max = p.val;
} else {
min = p.val;
max = q.val;
}
if ( min <= root.val && max >= root.val ) //1번 조건
return root;
if ( min < root.val && max < root.val ) { //2번 조건
return lowestCommonAncestor(root.left, p, q);
} else { //3번 조건
return lowestCommonAncestor(root.right, p, q);
}
}
}