What is Recursion
Definition
문제를 풀기 위한 접근방법중 하나로서, 함수 자기자신을 서브루틴 처럼 호출 하는 방식
Keywod
base case : 추가적인 재귀호출없이 바로 결과를 연산해 내는 case, 재귀 호출의 가장 마지막 단계를 수행하는 호출.
recurrence relation : 문제의 결과와 하위 문제들의 관계, base case에 도달 하기 위한 규칙
Example
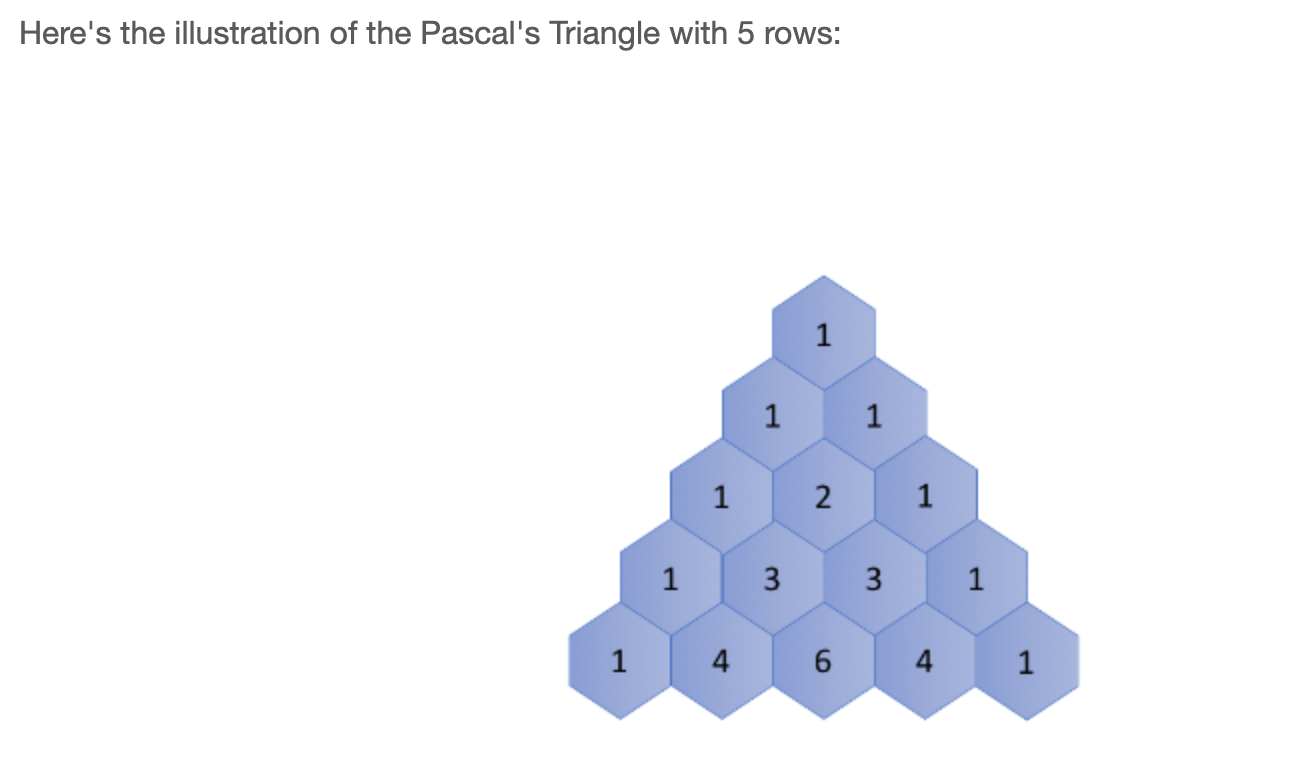
Pascal's Triangle이 재귀 호출의 기본적인 예시가 될 수 있다.
Pascal's Triangle은 삼각형 모양을 이루게 하는 숫자의 배열인데, 각 로우의 첫번째와 마지막번째의 숫자는 항상 1이고, 그 사이에있는 숫자들은 이전 로우의 바로 위에 있는 숫자와 그 앞 숫자의 합이다.
recurrence relation
Pascal's Triangle에서 i번째 로우의 j번째에 있는 숫자를 산출해 내는 함수 f(i,j)가 있다고 하자.
이때 다음의 수식을 이용해서 recurrence relation을 표현 할 수 있다.
1
f(i, j) = f(i - 1, j - 1) + f(i - 1, j)
base case
우측끝 과 좌측끝에 해당하는것들이 base case이다. 다음과 같은 수식이 된다.
1
f(i,j) = 1 where j = 1 or j = i
Memoization
재귀를 하다보면 중복 연산을 하게 되는 경우가 발생한다. 예를 들어 Fibonacci number같은 경우 다음과 같은 수식으로 구할 수 있다.
1
2
f(0) = 0, f(1) = 1
n! = f(n) = f(n-1) + f(n-2)
그래서 다음 예시로 중복 연산이 발생한다는것을 알 수 있다.
1
f(4) = f(3) + f(2) = (f(2) + f(1)) + f(2)
위 식 처럼 f(2)에 대한 연산이 2번 발생한다. 이렇게 되면 우린 이미 f(2)에 대한 연산을 한번 했는데, 한번 더 함으로써
불필요한 연산을 더 하게 된다. 위 예시는 4에 대한 예시라서 그렇지 만약 숫자가 더 커지면 중복 연산은 미친듯이 많이 발생한다.
중복 연산을 방지하기 위해선 한번 연산했던것에 대한 저장이 필요하다. 그것을 해결하기 위한 방법중 하나로 Memoization을 도입한다.
Memoization은 중간 결과값을 메모리에 저장하고 있는것으로 특정 Input에 의한 값을 저장 함으로써 다음에 동일한 Input이 왔을땐 연산을 하기 보단 저장해 놨던 값을
반환 하는 식으로 처리 한다.
1
2
3
4
if ( n is cached ) {
return cached result
}
return f(n-1) + f(n-2)